정보이론의 기초(Information Theroy)
런 길이 부호화 (Run-Length Coding)
가변길이 부호화 (Varibale Length Coding)
사전 기반 부호화 (Dictonary-Based Coding)
산술부호화 (Arithmetic Coding)
무손실 영상 압축 (Lossless Image Compression)

무손실 압축 : Encoder로 들어가는 Input data와 Decoder로 출력되는 Output data의 내용이 동일한 경우
손실 압축 : Encoder로 들어가는 Input data와 Decoder로 출력되는 Output data의 내용이 동일하지 않은 경우

B1 : 압축 후에 사용되는 비트 수 (분모) , B0 : 압축 전에 사용되는 비트 수 (분자)
=> 압축률이 4인 경우, 압축 후 데이터 크기가 원래 크기의 1/4이 된다는 의미입니다.
따라서, 압축률이 4일 때는 데이터가 25%로 줄어든 것이 아니라, 원래 크기의 1/4이 남아 있는 것입니다.
즉, 압축률이 4라는 것은 데이터가 75% 압축되었다는 의미
압축률의 숫자가 클수록 압축을 더 잘하는 것!


pi는 information source에서 나타날 확률 / log2(1/pi) - 자가 정보(self information, 최소한의 심볼을 나타내는 비트 수)
엔트로피는 각 심볼의 pi x log2(1/pi) 를 말하는 것

왼쪽 - 256레벨 grayscale image ( 0 ~ 255, 전부 나타날 확률이 동일한 값 )
오른쪽 - 256레벨 grayscale image ( 2개의 값만 존재 , 한 개는 1/3 또 다른 한개는 2/3 )

엔트로피와 코드 길이
엔트로피 η는 소스 S의 각 심볼을 코드화하는 데 필요한 평균 비트 수의 하한을 지정합니다.
즉, 어떤 인코딩 방식을 사용하든 엔트로피 값 이상으로 비트 수를 줄일 수는 없다는 의미

즉, 여기서 lˉ은 인코더에 의해 생성된 코드워드의 평균 길이(비트 단위)입니다. lˉ 이 η 에 가까울수록 압축 효율이 높다는 것을 의미
{ 대표적인 무손실 압축 방법 }
런 길이 부호화 (RLC, Run length Coding)
1. 기억이 없는 소스 (Memoryless Source): 독립적으로 분포된 정보 소스를 의미합니다. 즉, 현재 심볼의 값이 이전에 나타난 심볼들의 값에 의존하지 않습니다. (앞에 나온 확률이 뒤에 나올 확률의 결과값에 영향을 주지 않음)
2. 런 길이 부호화 (RLC)는 기억이 없는 소스를 가정하는 대신, 정보 소스에 존재하는 기억을 활용합니다.
3. RLC의 근거: 정보 소스가 심볼들이 연속된 그룹을 형성하는 성질을 가질 경우, 이러한 심볼과 그룹의 길이를 부호화할 수 있습니다. => 반복되는 심볼들을 하나의 그룹으로 묶어 압축할 수 있다는 것
{ 대표적인 엔트로피 코딩 방법 - 압축률이 가장 좋아야 됨 }
허프만 코딩 알고리즘 (Variable Length Coding, 가변 길이 부호화)
1. 초기화: 모든 심볼을 빈도 수에 따라 정렬하여 목록에 넣습니다.
2. 목록에 심볼이 하나만 남을 때까지 반복합니다:
- 목록에서 빈도가 가장 낮은 두 개의 심볼을 선택합니다.
- 이 두 심볼을 자식 노드로 하는 허프만 서브 트리를 형성하고, 그 위에 부모 노드를 생성합니다.
- 자식들의 빈도 합을 부모 노드에 할당하고, 목록의 순서가 유지되도록 부모 노드를 삽입합니다.
- 자식 노드를 목록에서 제거합니다.
루트에서 시작하여 각 리프(마지막 노드)에 경로를 따라 코드워드를 할당합니다.

허프만 코딩의 속성
1. 유일한 접두사 속성 (Unique Prefix Property): 어떤 허프만 코드도 다른 허프만 코드의 접두사가 아니므로, 디코딩 시 모호성이 없습니다.
2. 최적성 (Optimality): 최소 중복 코드(minimum redundancy code)로, 주어진 데이터 모델(즉, 정확하고 주어진 확률 분포)에 대해 최적임이 입증되었습니다.
- 빈도가 가장 낮은 두 개의 심볼은 마지막 비트만 다르게 하여 나머지는 같은 길이의 허프만 코드를 가집니다.
- 더 자주 발생하는 심볼(빈도 수 높은)은 덜 자주 발생하는 심볼(빈도 수 낮은)보다 더 짧은 허프만 코드를 가집니다.
- 정보 소스 S의 평균 코드 길이는 η+1보다 엄격히 작습니다. 식 (7.5)와 결합하면 l < η+1이 됩니다.




lˉ 는 평균 코드 길이
- 허프만 코딩의 평균 코드 길이 lˉ는 엔트로피 η와 거의 유사 / 그러나 k 값을 크게 설정하여 허프만 코딩을 개선하려는 시도는 심볼 테이블의 크기가 기하급수적으로 증가하여, 실제 응용에서는 비효율적이고 비실용적일 수 있다는 한계를 가집니다.

End of File을 받을 때까지 객체 내부에 함수 과정을 지속적으로 수행함 (계속 반복됨)
- 초기 코드 (Initial code)는 빈도 수에 대한 사전 지식 없이, 초기 합의된 코드를 사용하여 심볼에 할당됩니다.
- 업데이트 트리 (update tree)는 적응형 허프만 트리를 구성합니다. 기본적으로 두 가지 작업을 수행합니다:
- (a) 심볼의 빈도 수를 증가시킵니다 (새로운 심볼을 포함하여)
- (b) 트리의 구성을 업데이트합니다.
- 인코더와 디코더는 정확히 동일한 초기 코드와 트리 업데이트 절차를 사용해야 합니다.
- 노드는 왼쪽에서 오른쪽, 아래에서 위 순서로 번호가 매겨집니다. 괄호 안의 숫자는 빈도를 나타냅니다.
- 트리는 항상 형제 속성(sibling property)을 유지해야 합니다. 즉, 모든 노드(내부 노드와 리프)는 빈도가 증가하는 순서대로 정렬됩니다.
- 형제 속성이 위반될 경우, 교환(swap) 절차를 통해 트리를 재배열하여 업데이트합니다.
- 교환이 필요한 경우, 빈도가 인 가장 먼 노드를 최근에 빈도가 N+1로 증가한 노드와 교환합니다.
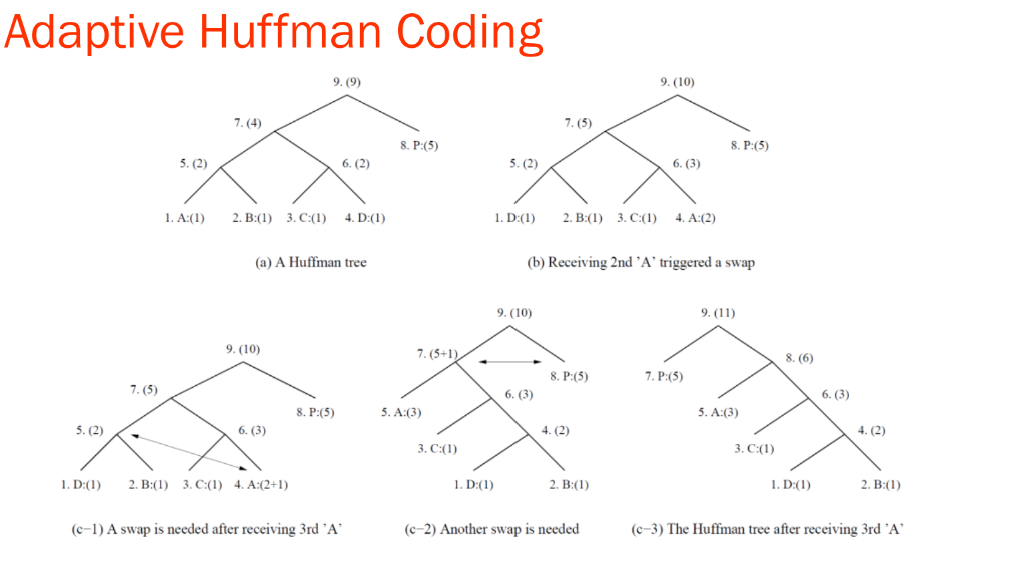
- 추가 규칙: 첫 번째로 전송되는 문자나 심볼은 특별한 심볼 NEW로 선행되어야 합니다.
- NEW의 초기 코드는 0입니다. NEW의 빈도(count)는 항상 0으로 유지되며(빈도가 증가하지 않음), 따라서 그림 7.7에서 항상 NEW: (0)으로 표시됩니다.

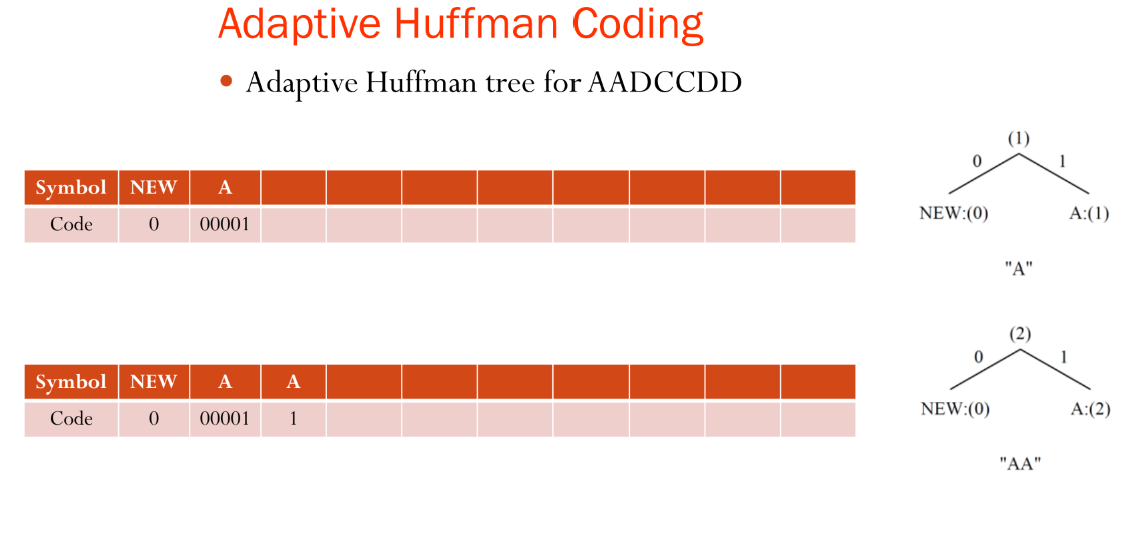

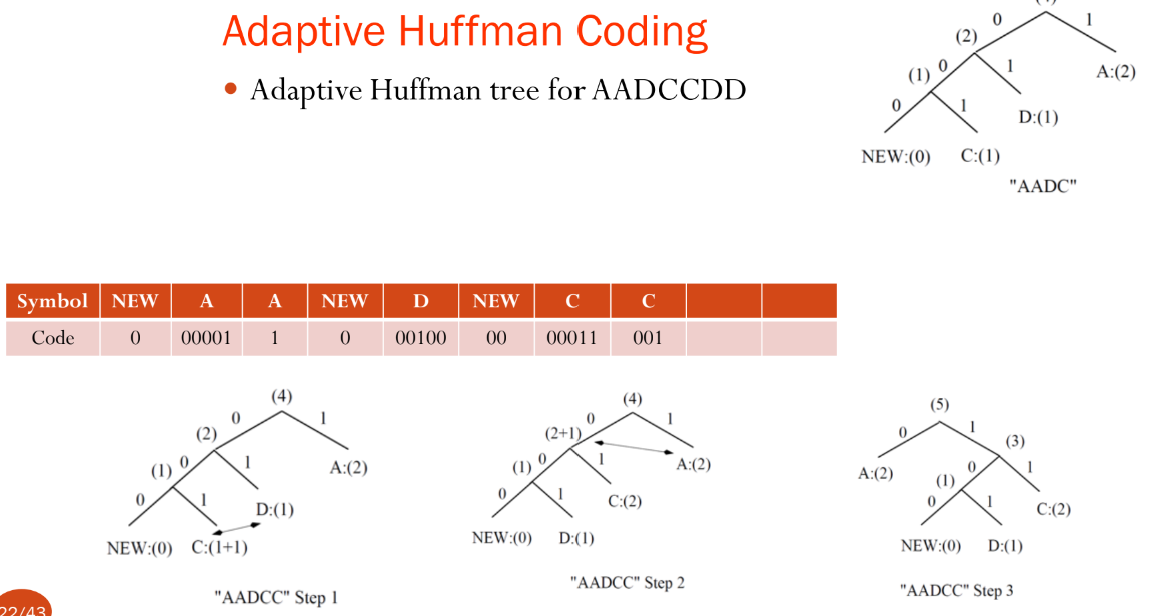
NEW는 항상 가장 왼쪽 리프 노드에 위치하게 됨, 부모 트리가 이동하게 되면 그 아래 서브 트리도 전부 따라오는 구조!
NEW 노드는 새로운 심볼이 나타날 때마다 트리에 삽입되는 구조로, 새로운 심볼이 등장할 때마다 해당 심볼을 NEW 노드를 통해 추가합니다.
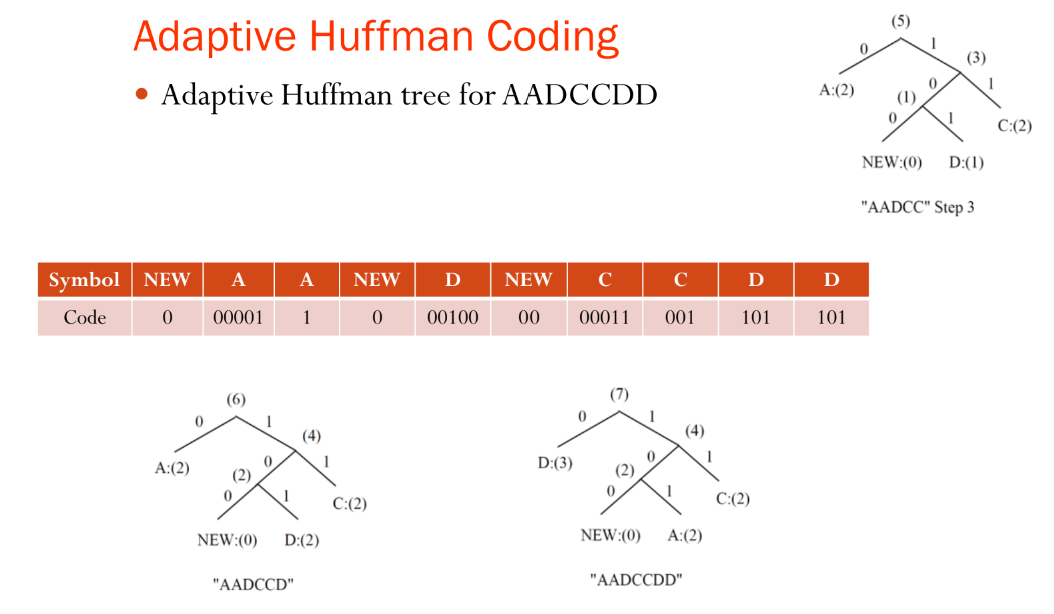

사전 기반 코딩(Dictionary-based Coding)
- LZW는 고정 길이 코드워드를 사용하여 자주 함께 발생하는 가변 길이의 심볼 / 문자열(예: 영어 텍스트의 단어)을 표현합니다.
- LZW 인코더와 디코더는 데이터를 수신하는 동안 동일한 사전을 동적으로 구축합니다.
- LZW는 더 길고 반복되는 항목을 사전에 추가하고, 이미 사전에 포함된 항목이라면 문자열 자체가 아닌 해당 항목의 코드를 출력합니다.


- 문자열 "ABABBABCABABBA"에 대한 LZW 압축 예제입니다.
- 아주 간단한 사전(또는 "문자열 테이블")으로 시작하며, 처음에는 단 3개의 문자만 포함되어 있고 코드들은 다음과 같습니다:
- 이제 입력 문자열이 "ABABBABCABABBA"인 경우, LZW 압축 알고리즘이 다음과 같이 작동합니다.
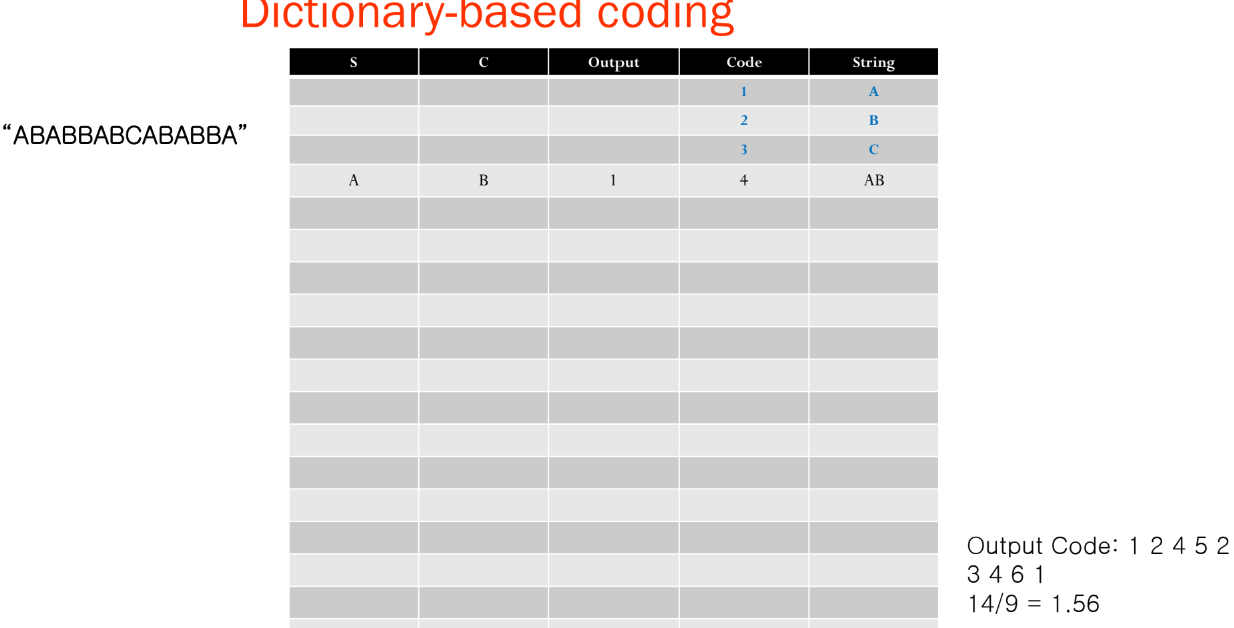
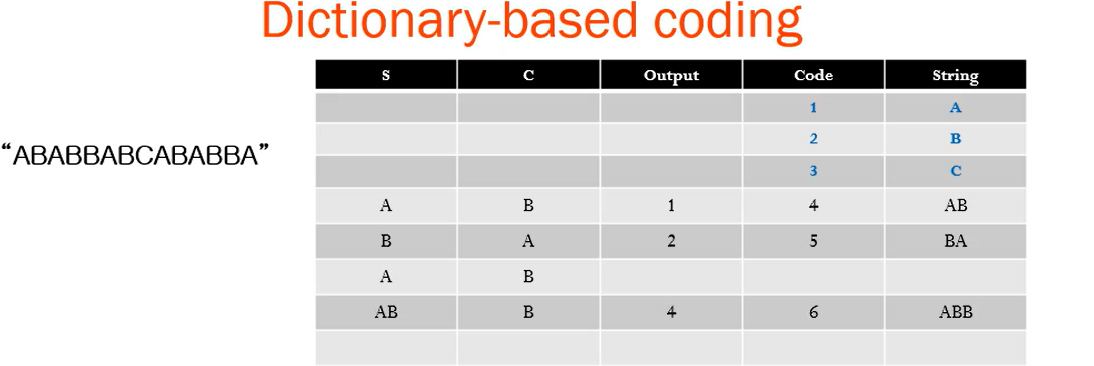
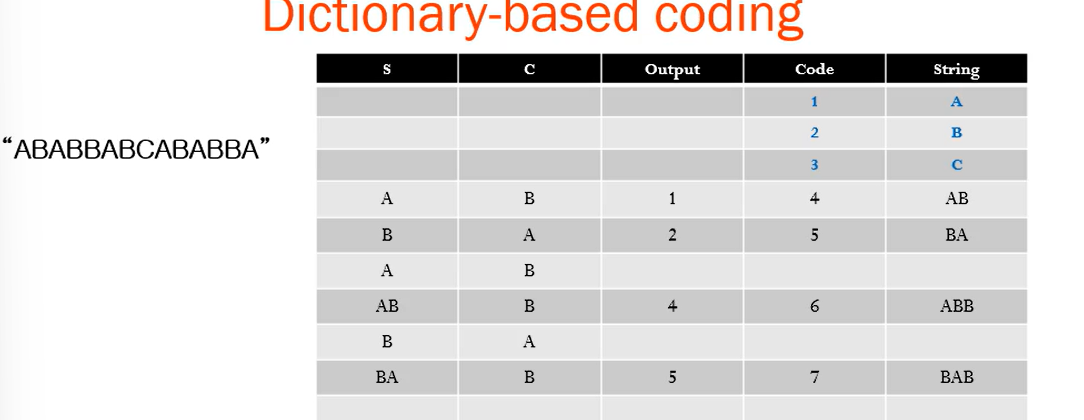

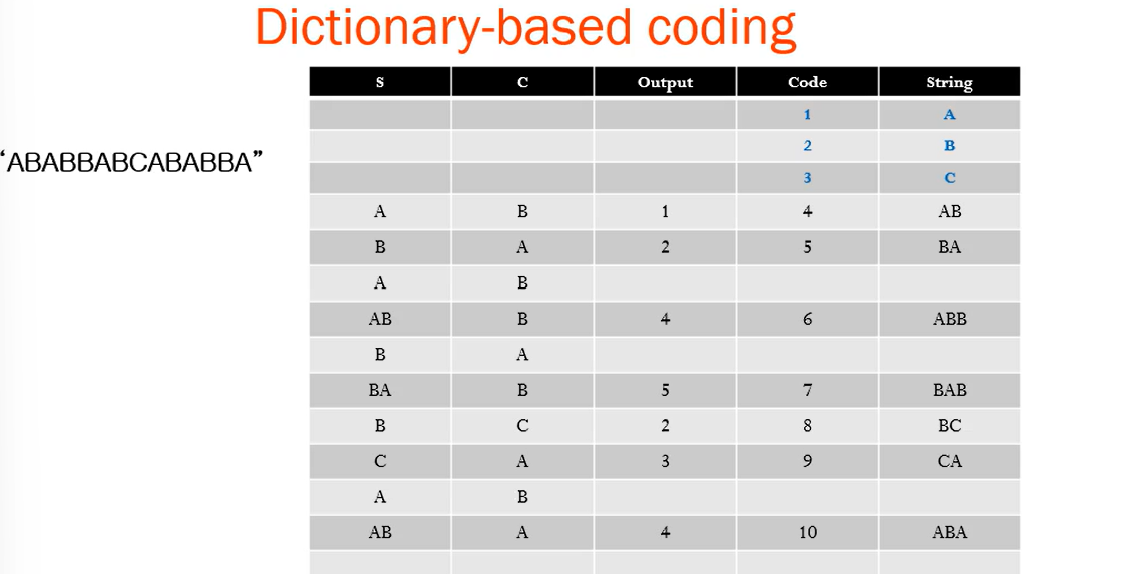
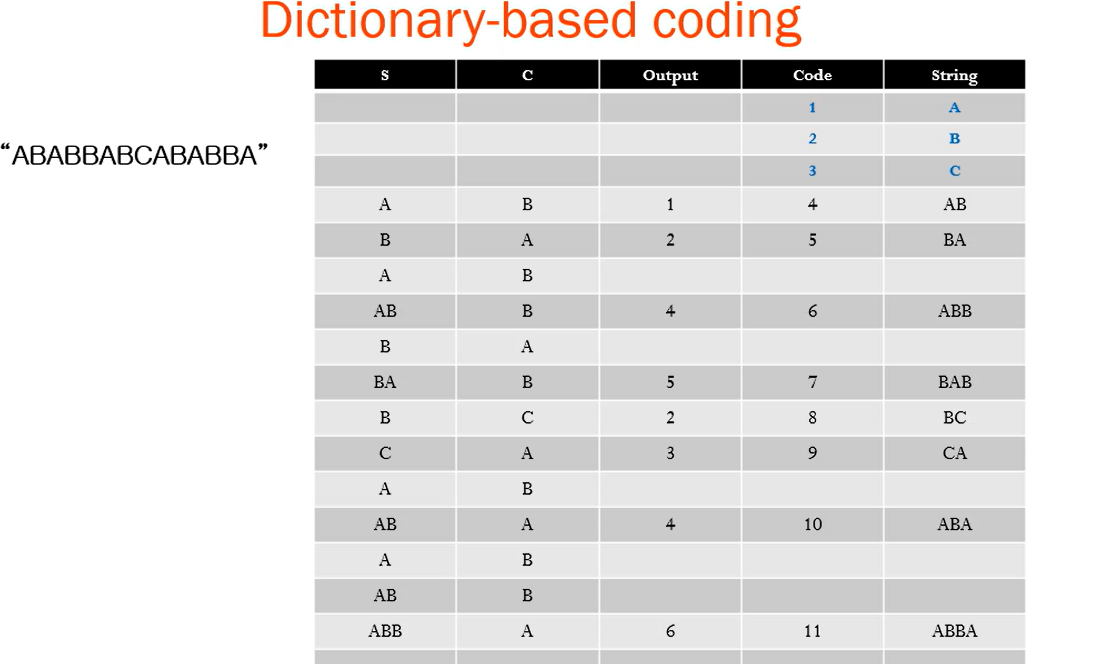
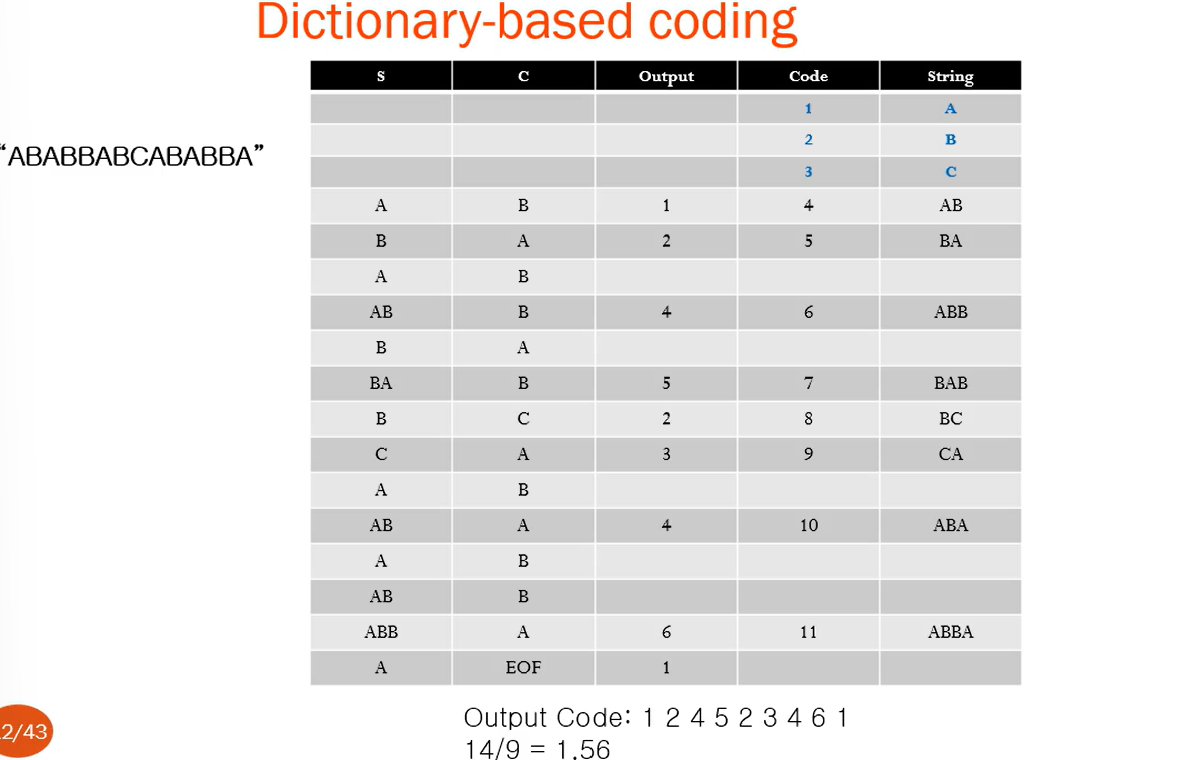
최종 output code :1 2 4 5 2 3 4 6 1
원래 문자열의 길이 : 14문자
압축된 코드 수 : 9개
압축률 : 14/ 9 = 1.56 압축률이 발생!
14개 중 Output Code는 9개이므로 1.56이 압축률이 됨

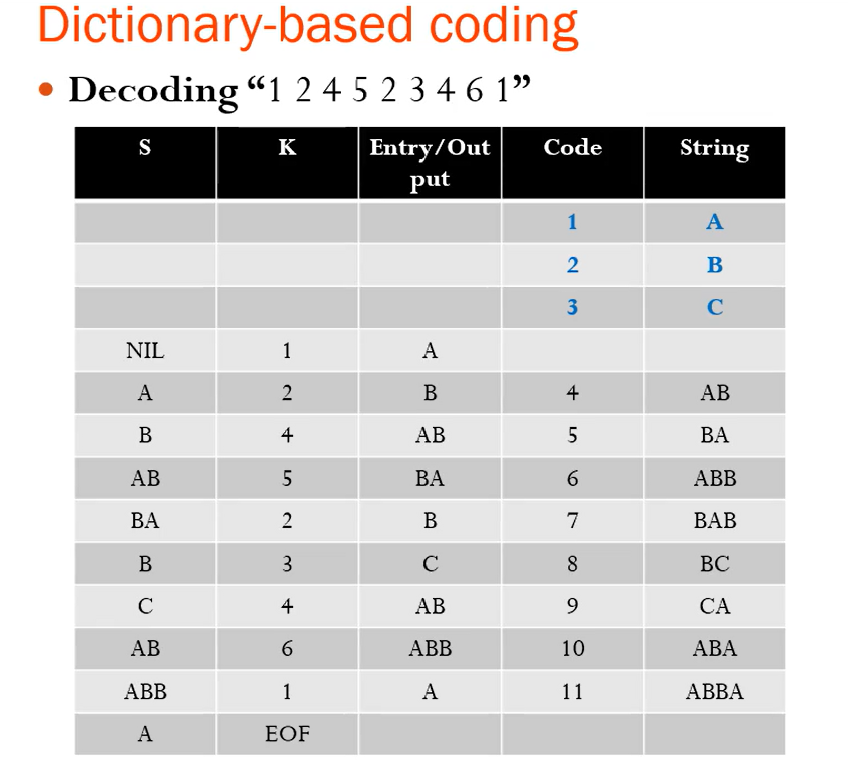
디코딩 결과 : ABBAABBBABBCBCAABAABBA

사전 기반 코딩(Dictionary-based Coding)
- 실제 응용에서는 코드 길이 l이 [l0,lmax]범위 내에서 유지됩니다. 사전의 초기 크기는 2l0입니다. 사전이 가득 차면, 코드 길이가 1씩 증가하며 이는 l=lmax에 도달할 때까지 반복됩니다.
- lmax에 도달하여 사전이 가득 차면, 이를 비우거나(Unix의 compress와 같이), LRU(Least Recently Used) 방식으로 가장 최근에 사용되지 않은 항목을 제거해야 합니다.
산술 코딩(Arithmetic Coding)
- 산술 코딩은 허프만 코딩보다 일반적으로 더 뛰어난 성능을 보이는 최신 코딩 방법
- 허프만 코딩은 각 심볼에 정수 비트 길이의 코드워드를 할당하지만, 산술 코딩은 전체 메시지를 하나의 단위로 처리할 수 있습니다.
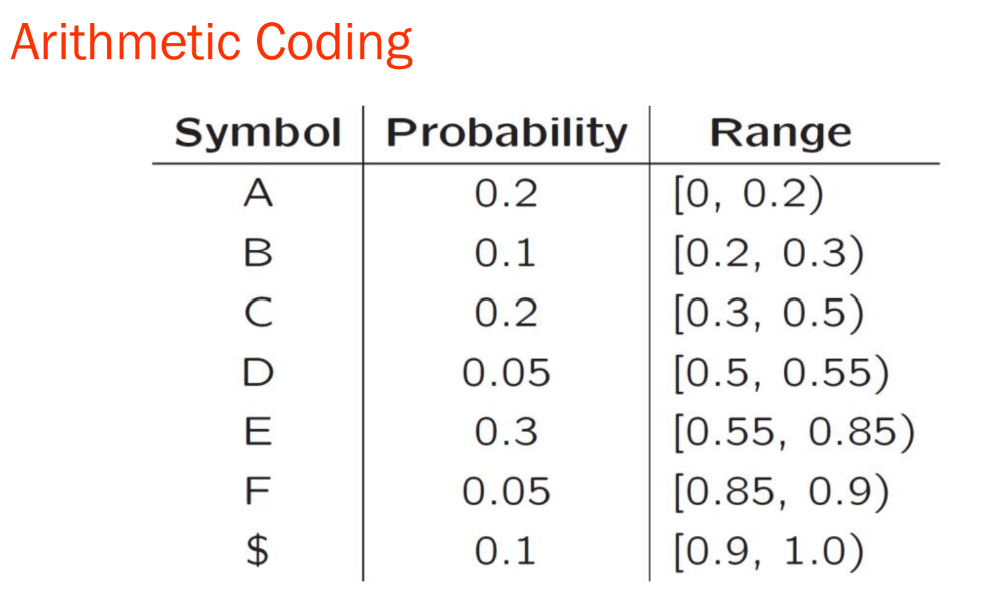
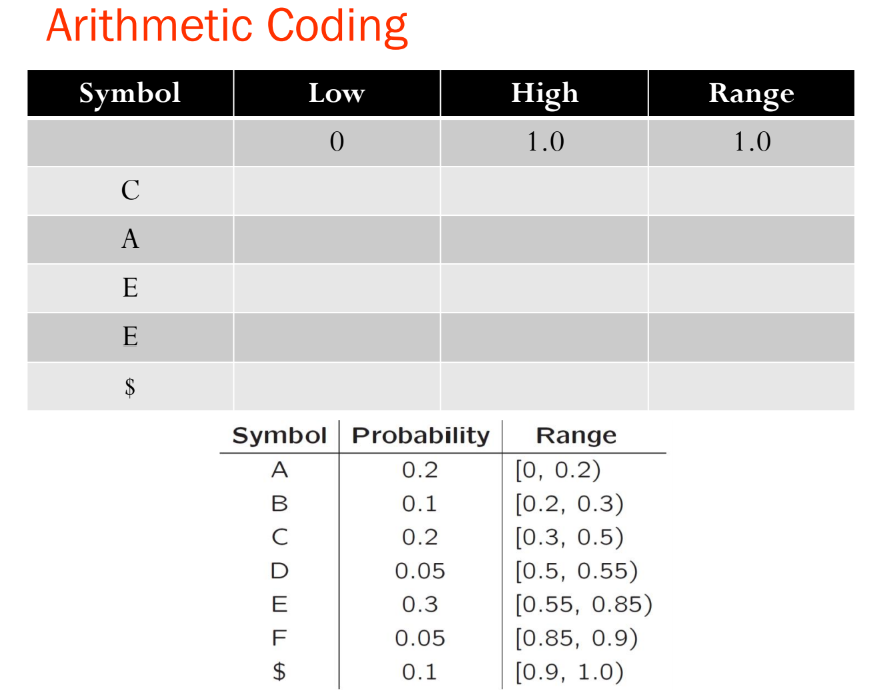
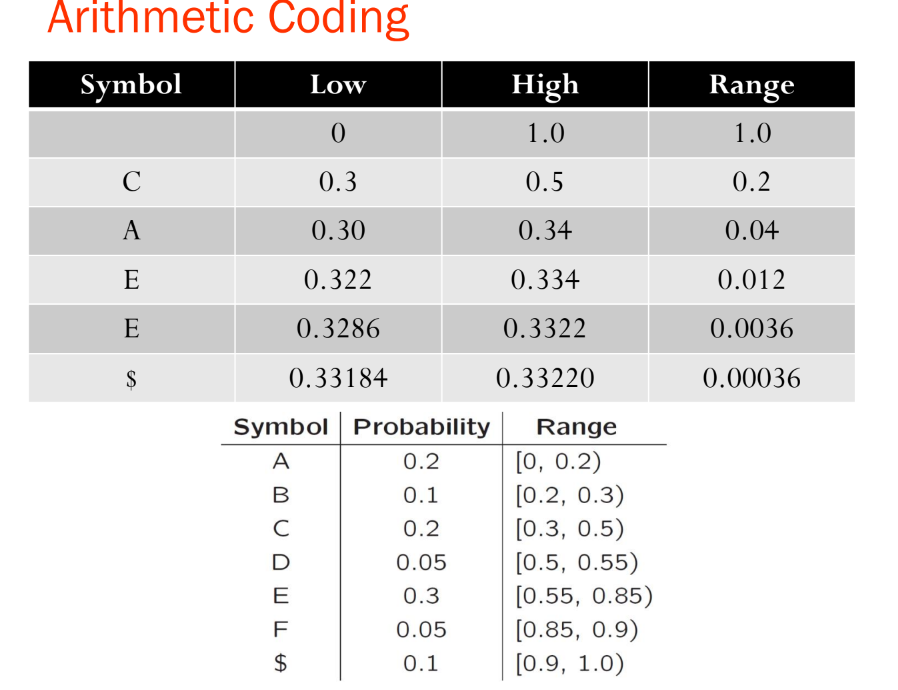
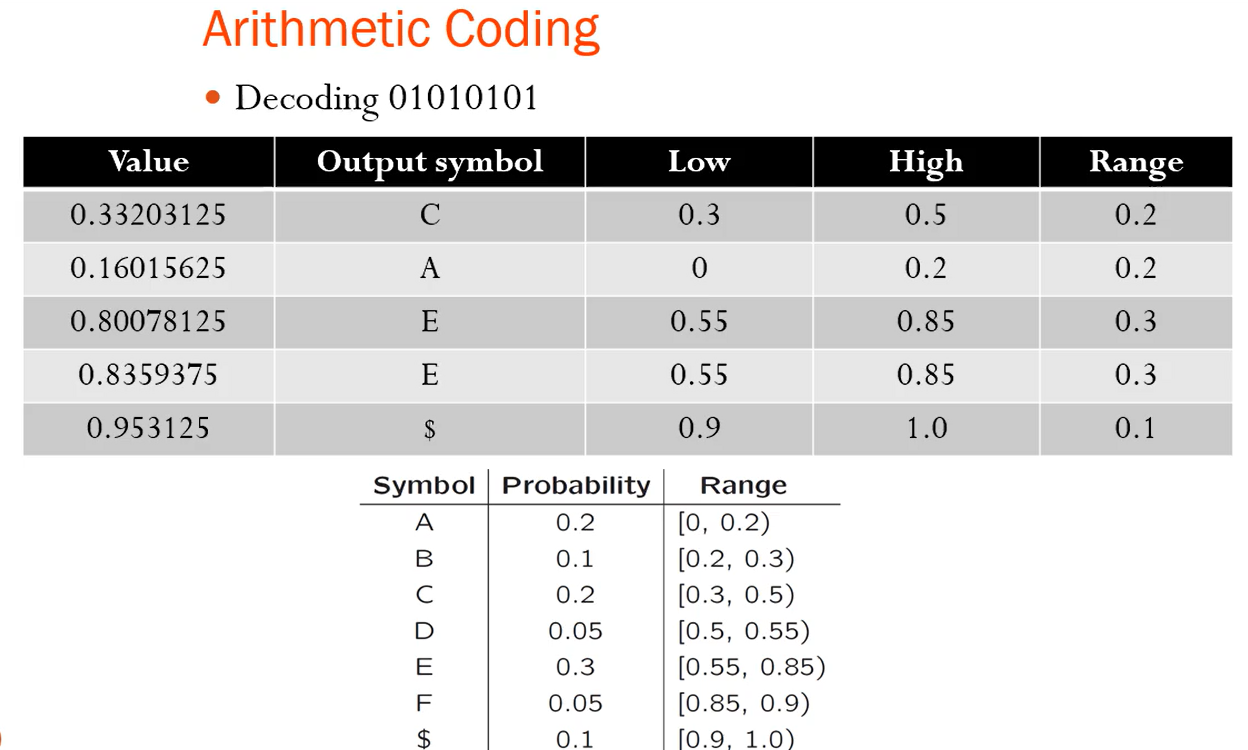
- 메시지는 반열린 구간 [a;b)로 표현되며, 여기서 a와 b는 0과 1 사이의 실수입니다. 초기에는 구간이 [0;1)입니다. 메시지가 길어질수록 구간의 길이는 짧아지고, 이 구간을 표현하는 데 필요한 비트 수는 증가합니다.

Range_low와 Range_high는 각 심볼들의 나오는 확률을 전부 더하면 1, 0과 1사이의 구간을 자신의 확률만큼 나누어 갖는 것 -> 각 심볼의 시작과 끝이 존재하는데 이때의 시작과 끝을 각각 Range_low와 Range_high임



무손실 이미지 압축(Lossless Image Compression)에서 차분 코딩(Differential Coding) 접근법

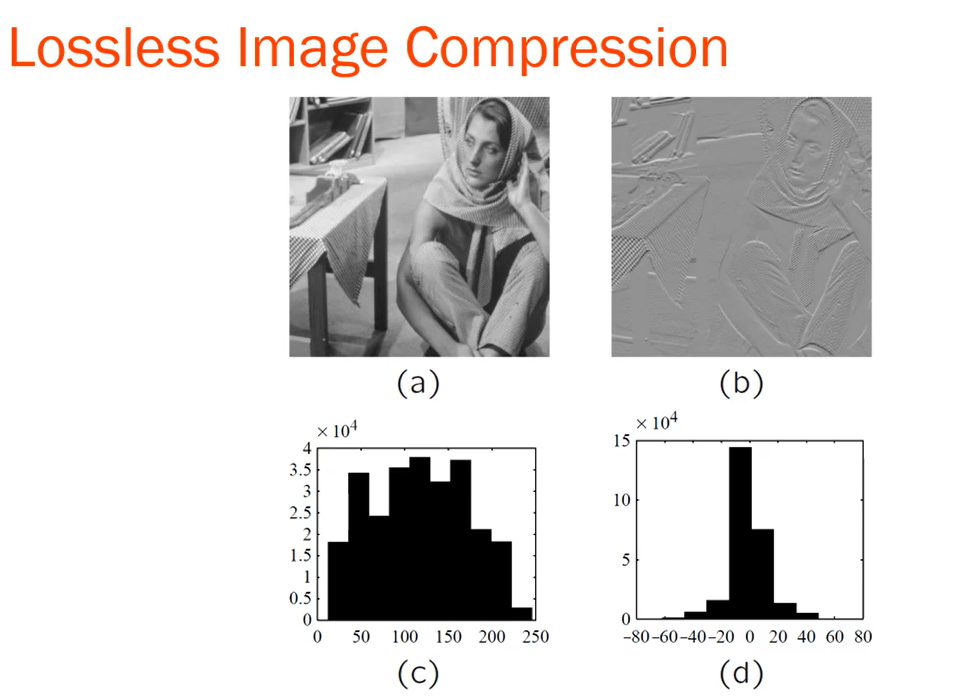
(b)는 (a)의 이미지에서 1픽셀 정도 이동한 이미지 - 아래에는 각각의 이미지에 대한 히스토그램(막대그래프) 값
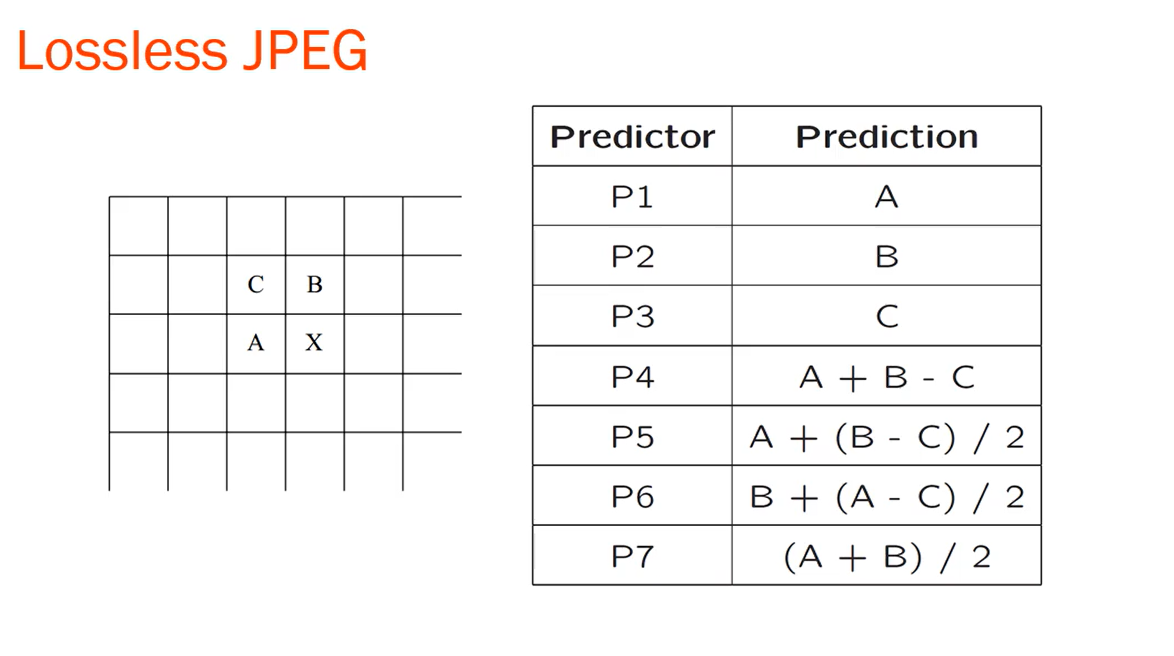
무손실 JPEG (Lossless JPEG)
- 무손실 JPEG: JPEG 이미지 압축의 특수한 경우입니다.
- 예측 방법 (The Predictive method):
- 차분 예측 생성: 예측기는 현재 픽셀의 예측 값으로 최대 세 개의 이웃 픽셀 값을 조합하여 사용합니다. 이때 현재 픽셀은 그림 7.10에서 'X'로 표시됩니다. 예측기는 표 7.6에 나열된 7가지 방식 중 하나를 사용할 수 있습니다.
- 인코딩: 인코더는 예측 값과 위치 'X'에서 실제 픽셀 값을 비교하고, 차이를 무손실 압축 기술(예: 허프만 코딩 방식)을 사용하여 인코딩합니다.

대부분의 경우에서 훨씬 높은 압축률로 손실 없이 압축할 수 있음
'Computer Science > 멀티미디어 공학' 카테고리의 다른 글
| 멀티미디어 공학 - 디지털 비디오의 이해 (0) | 2024.11.11 |
|---|---|
| 멀티미디어 공학 - 동영상의 이해 (0) | 2024.11.11 |
| 멀티미디어 공학 8주차 (컬러모델과 영상 포맷) - 기말고사 범위 시작 (0) | 2024.10.14 |
| 멀티미디어 공학 (7주차) (영상의 취득) (1) | 2024.10.09 |
| 멀티미디어 공학 (6주차) (영상의 인지) (5) | 2024.10.09 |